简介

最近在做一个Monte Carlo Tree Search的调研，这几年强化学习的热潮使得该算法大放光彩，我们在Alpha Go与Alpha Zero中也见识了它的强大。这篇总结本着存在必有其原因的思想，刨了下树搜索的发展历史，从发展中探讨MCTS的优点，也算是对自己这段时间调研的一个记录。

Tree Search

树搜索模型在MIP、GO、Constructive Algorithm、Search Engine等领域有广泛的应用，这里我把TS总结为如下过程：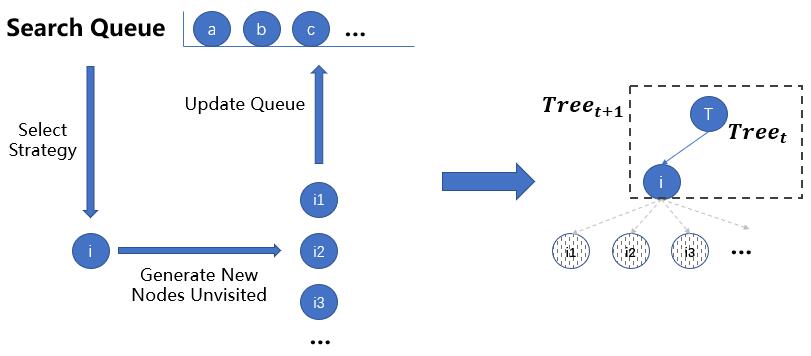
tree-search-introduction-image

Tree Search
存在一个Search Queue（SQ）储存待探索的节点，根据一定策略，每次选取一个节点进行探索，探索过程中会产生一些新的节点，更新SQ（将产生的新节点插入到SQ中），如此反复，直到满足终止条件
反复操作的结果是搜索树被不断完善，好的Select Strategy能加速搜索到optima的速度，结合剪枝策略（缩小搜索空间），进一步提高搜索效率
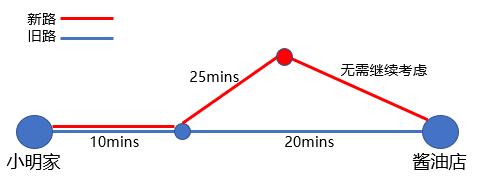
剪枝（prune）：当前节点的评估值差于整棵树已搜索到的最优值时，则放弃当前节点的后续探索步骤，将当前节点及其后续分支从树中剪掉，称为剪枝（PS：小明到酱油店间新修了一条路，他决定尝试是否能更快的到达目的地，历史上他走旧路需花30mins，如今他新路还未走完，所花时间已超过30mins，则可断定新路一定劣于旧路，即可放弃后续探索过程）

tree-search-prune

Uniformed Search不从环境中获取信息，属于较笨的搜索方式，树搜索中常见的类别有BFS(广度优先搜索)、DFS（深度优先搜索），这里用两张图简要回忆一下这两种搜索方式（序号表示搜索顺序）：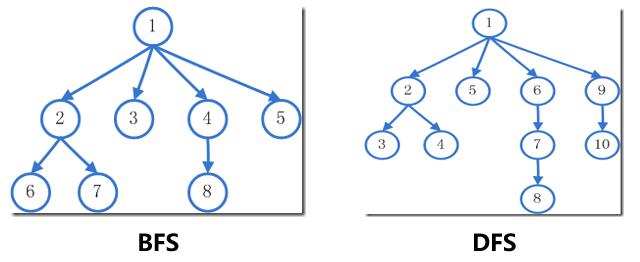
Bfs-and-Dfs

利用环境信息，辅助树搜索过程，提高搜索效率。这里我以A star算法举例说明：A star算法也是一种树搜索模型，常用于图论中最短路径问题；介绍时，我依以该经典问题作为背景方便理解，实际拓展中，自定义评估函数g(n)、h(n)（下文会介绍）即可用于其他场景。

A star
每个节点i保存两个信息：①g(i)记录start node到i的实际最短距离（已发生） ②h(i)记录i到end node的评估距离（未发生）
在Search Queue（SQ）中选取探索节点的策略为min{f(n)}，其中f(n)=g(n)+h(n)；由定义可知，f(n)用于衡量当前节点的总体评估距离，即利用了已发生的信息，同时利用了未知的预测信息
优点：算法灵活性高①当h(n)小于actual distance(n,end node)时，搜索的点较多，搜索范围较大，找到global optima的概率增大，但搜索效率较低（A star的prune也是以f(n)作为评估，h(n)较小时，节点被剪枝的可能性降低）；反之当h(n)大于actual distance(n,end node)时，搜索效率虽然提高，但更多时候搜索到的仅仅是local optima ②经典的A star算法中h(n)是静态的，实际中可将之设计为动态，随着搜索过程的进行，环境信息的增加，更新h(n)，提高后续搜索效率
缺点：①算法对h(n)的设计具有较强依赖性，h(n)与实际值越接近，算法搜索到global optimal的总体效率越大 ②不能保证一定搜索到global optimal

Monte Carlo Tree Search