实习部门的研讨会一直在推动Deep Learning的学习，但最近的几次交流学习方向有点被带偏了，故对于这一块的学习我只能按照自己的计划来走了。看资料的过程中，发现内容良莠不齐，故希望借此文章记录自我的学习过程，一方面将精辟的学习资料进行保存，另一方面督促自己对于这一块的进一步学习。

1.BLOG

1.1零基础入门深度学习

此系列是好朋友推荐的，简短的介绍了机器学习的一些基础，之后马上开展重点关注的CNN、RNN等，文章从实例到理论再到Coding，以开发人员的角度介绍知识（这里承认本人数学功底一般，直接上公式立马晕）。

已看完

零基础入门深度学习(1) - 感知器
零基础入门深度学习(2) - 线性单元和梯度下降
零基础入门深度学习(3) - 神经网络和反向传播算法
零基础入门深度学习(4) - 卷积神经网络
零基础入门深度学习(5) - 循环神经网络

证明过程看着有点懵，这种从特殊推到一般的形式简直是我的救星（虽然最后还是passing this section）
“深度循环网络”计算方式个人认为有点问题，从给定的图片可以看出，layer_index>1的循环层每个神经元应该受三个节点的影响，但是公式的意思仅表示其受两个节点影响，可能是书写错误

section-5_revise_1

零基础入门深度学习(6) - 长短时记忆网络(LSTM)

LSTM被发明出来的原因是因传统的RNN容易发生梯度消失 or 梯度爆炸，因为对参数的训练是沿着梯度的反方向，梯度消失即梯度趋于0，每次训练时，参数基本不发生改变，造成当前时刻输出基本不受长时间间隔的输出影响（几乎无依赖关系），这是不希望看到的；梯度爆炸的解释刚好相反，参数训练时，与当前间隔越长的N，其参数改变值会指数增长，也会阻碍训练过程

未看完

零基础入门深度学习(7) - 递归神经网络

2.实现

我对这一块尝试上手的方式就是实现别人的代码，对于不懂的函数再查询官网的文档，按需理解。刚好一个朋友对CNN这一块较熟悉，很多不懂的问题都有请教他，我阅读的代码就是它写的用CNN实现MNIST数据集手写书字体识别。
MNIST数据集是开源的，每一条数据都是一个手写的数字图像（0-9），大小是28*28的黑白像素（平铺后即为576个binary值）。因此这个问题本质上是一个多分类问题，希望训练一个模型，能精确的判断输入的手写数字到底是多少。
诺亚方舟实验室的服务器还是很赞的，很多环境早已配置好，因此我很开心的跳过了“学习死于安装”这一过程，下面的内容主要记录实现中自己的一些发现。

2.1参考材料

卷积神经网络实践之MNIST手写数字体识别——Xijun LI

Keras文档

2.2实现记录

input_shape
Keras中仅第一层需要加这个属性，后面的层会自动计算。需要注意的是属性值的格式，因keras是对Tensorflow及Theano的再封装，但因Tensorflow与Theano的语法存在差异，所以keras封装后不能做到语法完全通用。
我在实现时开始总提示error，后来定位原因是因两次实现的服务器中，keras后台依赖有差异（一个是Tensorflow，另一个是Theano），两者对输入数据的格式存在差异（一个希望label在前，一个希望在最后），做如下修改即可：

Mnist_code

画图
下载的数据都是binary值，不够直观，所以我接触数据的第一件事就是把它画出来，画灰度图的方式还是很简单，这里仅提供记录即可。
用numpy把数据reshape成28*28的格式，再调用pyplot中的imshow()即可，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
train_df = pd.read_csv('dara/train.csv')
train = train_df.values # Numpy representation of NDFrame
img_rows, img_cols = 28, 28
trainX = train[:, 1:].reshape(train.shape[0], img_rows, img_cols)
plt.imshow(trainX[img_id], cmap = plt.cm.gray) # 灰度图
plt.show()

3.公开课

前两章的内容将我领进了Deep Learning这个神秘世界，我学东西的特点是先消除神秘感，再系统性的学习内容，一方面提高学习效率，另一方面也能消除我看教材时有种打开英语课本第一页的心情。

对比了一些公开课与教程，我最终选择了Stanford的Convolutional Neural Network for Visual Recognition，课程的前半部分也对Machine Learning的一些基础知识做了回顾，让我对之前的一些黑盒式理解也更加清晰。

学习方式：介于视频是全英文授课，所以我是先看完GitHub上的课件，再看公开课进行补充。福利是原课程的视频被人copy到B站上了（无字幕版），有雷锋同志也翻译出了字幕版（有字幕版）。

3.1 学习笔记1——正则化

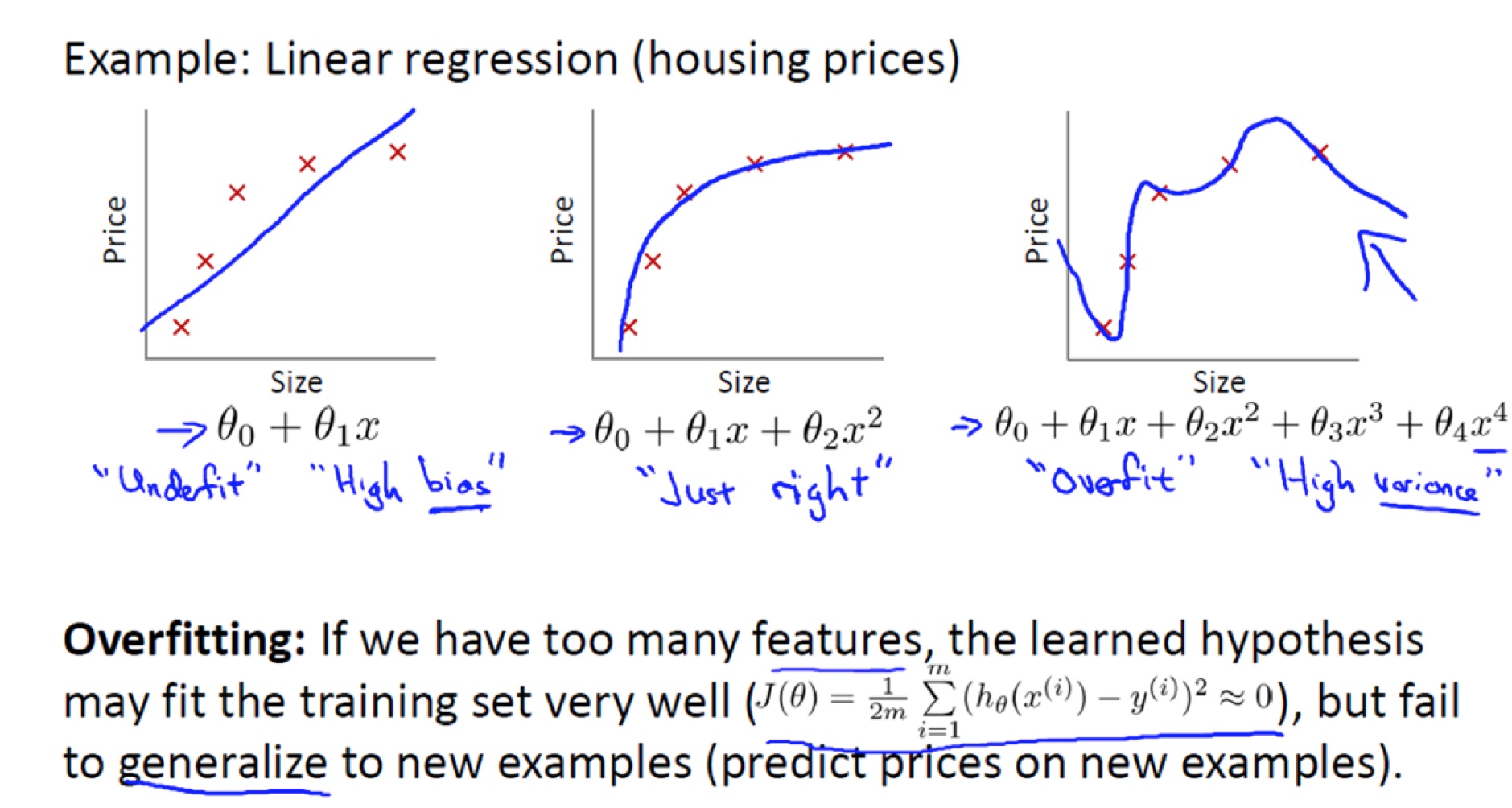
官方解释：在Loss Function中加入正则化惩罚项的作用是降低model的复杂程度，增强其泛化能力（在测试集[未知环境]的表现能力）。记得第一次接触这个概念时，是看的Coursera上的一门《Machine Learning的课》，当时用于解释的图与吴恩达老师公开课上使用的类似，如下：

Regularization Explanation

解释中，在损失函数中加入正则化项后，能让最终模型从model3（图3）转为model2（图2），也正是因为说明，我的理解就一直存在误区，认为正则化惩罚项的目的是降低模型中高维度项的参数值，低复杂度等价于用低维度项来进行拟合。

看了公开课中关于正则化的解释后（直达链接），特别是L1 Regularization与L2 Regularization的对比，发现与之前的理解存在矛盾。L1的目的是希望特征影响稀疏化，L2的目的是希望特征影响平均化，这两者加入目标函数中都不能使得model训练向低维度特征的稀疏化发展（L1可能导致高维度特征被保留、L2排斥这种稀疏化结果）。

经过自我探索，对这一块的认知有了新的理解，总结如下：模型的简单化是指参数的大小综合下降，而不是从维度上用更低次的项去拟合（L1与L2等Regularization方式都能达到该目的）；实际中，有些场景希望能用较少的特征来解释实际现象（倾向于用L1）,有些场景则希望尽量用上所有的特征（倾向于用L2），此时就需要根据经验来选取。

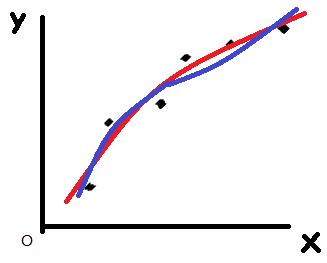
补充：降维以消除过拟合是从特征个数的角度出发（在考虑加入哪些特征时考虑的事情），而不是针对幂级数高低

PS：参数值的综合减小会使得模型更加简单（Linear Model中表现为曲线更加平缓），而不是高次项的参数比重减小。下图中，使用线性分类器做分类，在损失函数中加入L2正则化项，得到蓝线（y=49.7x + 0.159x^2 + 0.002x^3，较低的正则化超参）与红线（y=2.581x + 0.157x^2 + 0.008x^3，较高的正则化超参），发现参数综合值较低的曲线（红线）更加平缓，但高次项不一定更低。

Example Regularization

给出一个对过拟合/欠拟合、方差/偏差解释较全面的博客（直达链接），里面的解释中最让我受益的是随着model complexity的增加，在测试集上的表现为：variance逐渐增加，bias先减小后增加。起初，模型类似于随机预测（under-fitting），故在训练集、测试集上的预测都不会太好，因此bias大，但预测很稳定（所有的预测值差距不大），故variance都小；随着模型复杂程度的增加，模型挖掘数据内在分布的能力逐渐提高，因此在训练集与测试集上的bias都变小，但预测的点的差异化也逐渐表露，故variance增加；当模型复杂程度进一步增加时（over-fitting），模型较依赖于训练数据，训练集毕竟只是真实情况的一个采样（与真实情况存在一定差异），故在训练集上的bias虽然继续减小，但在测试集上的bias却增加了，此时variance因预测点的差异化的提高而继续增加。