Operation Research and Machine Learning
实习期间研究的方向之一就是如何将machine learning的技术与运筹学结合,加速求解过程,运用到华为供应链场景。依据这个突破点,外加自身对这一块有着浓厚的兴趣,故查阅了近几年结合的研究进展,发现在运筹学传统的技术上,一旦加上learning,就可以投较好的期刊或会议,如《A machine learning -based approximation of strong branching》——INFORMS Journal of Computing、《learning to search in branch and bound Algorithms》——NIPS…
不难看出,这一研究领域是未来学术界与业界的热门方向,因此本文将自身的理解、学习进展进行记录与分享。
1.运筹学与机器学习的区别是什么?
此问题是Noah Lab实习面试中,leader的问题之一。当时我给出的回答是:“机器学习侧重于从数据中挖掘潜在分布,以响应未知领域,关键是拟合;运筹学则侧重于对问题的抽象,建立能精确描述问题的数学模型,并利用相关算法求得最优解。”leader追问:“机器学习问题也要建立数学模型,为什么它求得的总是有误差,是近似解,而运筹学中能求得最优解呢?导致这种差异的本质是什么呢?”说实话,我后来就有点懵圈…
那时刚接触机器学习,侧重于了解算法。知道机器学习中的经典模型有逻辑回归、SVM、决策树,求解算法有梯度下降(逻辑回归)、最大信息增益(Tree model)、BP(神经网络);运筹学中的经典模型有TSP、Knapsack、Bin Packing、Scheduling,求解算法则包括启发、元启发、超启发、精确解算法等等。当时没从结合上去理解,总觉得是截然不同的内容,了解深入后,才发现都是一个套路,万变不离其宗——数学。
这里我先给出我的结论,后序做详细的解释:
定义:区分机器学习与运筹学的关键在于先验知识的强弱,依据其差距,两者产生了各自的方法论。
了解异同点之前,补充一下求解问题的通用范式:建立数学模型(问题抽象)→获取数据→设计求解算法(问题求解)→结果分析与评估
1.1.模型层面
现实问题可大致分为两类:离散优化与连续优化。运筹学的研究范畴中,两者都包含,考虑到其发展背景,研究的问题(模型)大多包含众多复杂的限制条件(约束),且其中以离散优化问题居多(即组合优化);机器学习则侧重于连续优化(问题本身离散时,建模时也会尽量将解空间松弛为连续域),期望拟合一个分布,模型中一般不包含约束(少量模型存在约束,如SVM)。
机器学习相关问题中,对问题内在结构了解较模糊,因此仅能借助于数据驱动的方式,期望从数据中挖掘出问题的潜在分布,便于管理者做决策。而运筹学问题中,问题限制能被描述为一条条的数学公式(等式与不等式),解空间(问题结构)已经被公式所限定,所做的问题是如何在其中找到最优解,因此具备更强的先验知识。
举例说明:
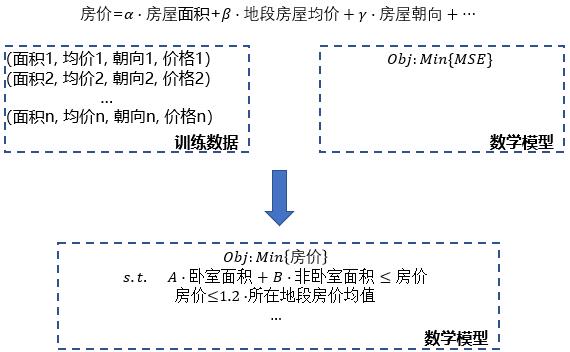
Example_1.假设现在我们要预测某个房屋的价格,方便做出是否购入的决策,传统机器学习的做法是收集数据,提取特征(房屋面积、地段房屋均价、朝向等等),然后建立房价预测模型(以最小化LOSS为目标的连续优化问题),训练参数,最后将需预测的房屋的相关数据录入到训练好的模型中,得到预测的房价;若现处于上帝视角,能清晰知道房屋的价格与各因素的关系,如:价格不小于卧室面积的A倍与非卧室面积B倍之和,同时价格不会高于地段房价均值的1.2倍,又因我们是购买者,期望以最小成本完成购买任务,因此目标是最小化房价。
第一种方案求得的解较难验证,第二种则一定是存在于解空间中的最优状态,故对问题内在结构很清晰时,第二种更优。
Example_2.装箱问题是运筹学中的经典问题,现存在一些长宽高不等的item与同质的箱子,期望以最小的箱子个数将item装载完。看到这个问题,很多人会觉得不难,毕竟该问题的数学模型已被学者们研究得十分透测,考虑箱子内在装载结构,以item被装载时不超过箱子边界(overlap)为约束,最小化箱子使用个数为目标,有基本model、set cover model等形式。问题该类表达中,一个大前提是item与箱子的基础数据(长宽高)皆已知,这是一个很强的先验知识。若现在问题改为长宽高数据未知,要如何处理呢?从机器学习的角度看,若能获取历史装箱数据,即:(m1个item1,m2个item2,m3个item3,…,n1箱子数),基于此数据构造特征(item总长、总宽、总高…,n1箱子),建立二分类问题(1:可装完 / 0:不可装完),训练二分类模型,之后便可将新item的数据转换为特征,将箱子个数特征上从0开始不断增加1,当model第一次输出1时,即为输出的最小的箱子使用个数(或直接建立以箱子个数为label的预测模型)。
从例子中可看出,运筹学中在抽象实际问题时,具备更多的先验知识,得到的解更能被接受。
两者研究的问题基本都是NP-Hard问题,如运筹学中的TSP、Bin Packing等,机器学习领域中的KNN、Decision Tree Model等等。
1.2.算法层面
我们在两个领域内总能听到不同的算法,运筹学中,当问题需求得精确解时,线性规划中的单纯形法,整数规划中的DP、Branch and Bound、Cut-Plane算法往往听的比较多,求较优近似解时,则是进化算法、SA、Tabu Search等。而谈到机器学习,则有梯度下降、SMO、信息增益(ID3)、Lloyd Algorithm(KNN)等等。
算法层面上,两个领域的知识是相通的,因为所有的算法其实无外乎两类,精确算法与近似算法。
补充:对各种算法进行划分时,需结合求解问题的背景,如问题的解空间为凸时,梯度下降法可求得全局
,属于精确算法;但解空间非凸时,梯度下降法仅能求得一个局部最优解,此时属于近似算法。
精确算法是聪明的暴力搜索,指导好的搜索方向,当搜索到劣质的解空间时,及时制止。
精确算法在机器学习领域中听的比较少,原因在于问题规模往往较大(数据量大),在有限的计算资源下,很难求得最优解,因此近似优化算法居多,更多的研究方向在于针对特定的模型,如何改进优化算法,使求得的解更好。常用的思路是增加算法的随机性,在收敛能力与随机上做好trade-off,随机性的带入能在搜索中辅助跳出局部最优,但随机性过多带入会导致算法的搜索能力较弱,与random searching无异。这里给出一篇网上的博客《梯度下降优化算法总结》,介绍梯度下降法的改进策略,便于理解上述提到的trade-off。
运筹学领域,精确算法往往只能在中小规模问题上发挥作用,但由于该类算法能给出BOUND(即使在有限时间内无法求得最优解,通过Branch and Bound等算法也能返回问题较优的上(下)界,即全局最优解的极限值),且十分方便做并行化,故受一些学者青睐。大规模问题上,现阶段还是近似算法更被看好,如Hill Climbing等,为防止算法过早陷入局部最优,也会往其中增加随机性,如Tabu Search中的禁忌策略、GA中的变异及种群多样性维持策略、ACO中路径选择一般采用轮盘转法等等(GA、ACO等都属于仿生算法,是一种搜索框架,框架本身具备一定收敛能力[玄学…],在设计时往往添加适合问题的operator并融入随机性)。
因此,从算法层面分析,两者设计思想基本等同,权衡收敛能力与随机性之间的trade-off
补充:精确解中也存在两者的权衡,如分支定界算法中分支策略的选取,后续描述会提到。
1.3.小结
机器学习与运筹学的主要区别?——先验知识的强弱。
机器学习问题结果为什么总存在误差,运筹学却能求得精确解?——先要明确有误差不等同于没找到精确解,且运筹学中也会存在误差。机器学习中,当数据量较大时,难以求得精确解,会造成误差,但即使求得了精确解,误差也是存在的。原因在于先验知识的缺少导致问题从数据建模(按先验知识给定的模型与实际可能存在一定差距),并且用模型做泛化时,未知信息进一步增加,这些都是导致误差的原因。运筹学的模型是从解的结构出发,约束能正确描述解空间的区域,求得精确解,但该解不一定是实际需求完全对应(问题的抽象可能存在一定误差),复杂问题的规模较大,可能得不到最优解(MIP-Gap),因此存在误差也是可能的。
复杂度层面,机器学习的规模来源于庞大的训练数据,运筹学则来源于问题描述的复杂度(大量约束、复杂目标…),求解算法的设计套路类似。
广义上,有人认为机器学习是运筹学的一个应用领域链接直达;更广义的说,都是数学…
2.谈一谈最优解与较优可行解
2.1.最优解
求得现实问题的最优解是件较困难的事。
有人会问,上述讲解算法分类时不是有精确算法这一说吗,当我们得到问题的抽象模型后,利用精确解算法,即可得到问题的最优解。但关键问题有两点:a.抽象的数学模型是否能真实反映实际;b.能否在有限的计算能力下求得问题的全局最优解。
针对a,这里引入一句很精炼的总结,出自中科大教授唐珂来华为介绍演化计算时,slides上的一句话:
“用数学规划,求近似问题的精确解;用演化计算,求精确问题的近似解”——唐珂
演示时以机器学习中的二分类问题为例,很容易得知二分类问题的损失函数是阶梯函数(分类True or False),但因该函数不可导,故用sigmoid函数进行替换;此操作后,我们实际求解的问题即为原问题的一个近似问题,我们还需要验证近似问题的最优解与原问题的最优解相对应才行。问题抽象的难度来源不仅仅是目标函数,约束有时也难以定义成表达式或定义成表达式后无法用数学规划的方式求解,如:A >= B xor (C and D)…
再来说b,当问题的变量、约束较多时,解空间过大,在有限的计算资源下,精确解算法很难求得最优解,因此一般的Solver都会提供提前终止搜索的接口,如Time Limit或者Max Gap(Upper Bound与Lower Bound之间的差距小于给定阈值时停止搜索),此时求得的解也不是全局最优解。
2.2.较优可行解
较优可行解的求解方式灵活很多,但得不到Bound的它就没有终极目标——一只努力拼搏却缺乏一丝灵魂的奋斗者。
上述已提到过近似算法的设计核心,即收敛能力与随机性之间的权衡。较优可行解往往在工业界接受的比较多,企业更多的关心是当前算法比前一版本提高程度,同时,技术人员的最优与业务人员的最优往往存在差异。
3.Machine Learning与Operation Research结合举例
哪里有计算开销大的地方,哪里就可尝试使用learning做近似,训练一个evaluation function
3.1.In Exact Algorithm
Branch and Bound中,好的树节点搜索顺序能使得Bound收敛的更快,加速剪枝过程,从而提高求解效率,传统的方法有广度优先、深度优先等,《learning to search in branch and bound Algorithms》则学得一个自适应的searching order。
Branch and Bound中,分支策略尤为重要,尽可能保证分支两侧的解空间均匀,且具有更好的Bound,好的分支策略往往需要高计算开销,《A machine learning -based approximation of strong branching》、《Learning to branch in mixed integer programming》、《Towards Learning Integral Strategy of Branch and Bound》…皆提出学得一个branch strategy的evaluation function出来,加速该过程。
以decomposition(Dantzig-Wolfe)为依托,《Learning whe to use a decomposition》。
以Column Generation为依托,用trained model生成pricinng problem的近似,并做出修正。
Reinforcement Learning
3.2.In Heuristic Algorithm
- 《Small Boxes Big Data: A Deep Learning Approach to Optimize Variables Sized Bin Packing》中,用neural network训练一个分类器,输出对当前算例所执行的最好的启发式算法的编号(训练数据中实现了八种启发式算法,以最优算法编号作为label)。