GUROBI是现阶段求解效率最高的商业最优化求解Solver，与之类似的还有CPLEX、LpSolve、Lingo等，介于研究生与实习期间对该类Solver接触较多，了解到合理使用Solver对求解效率的影响之大，故希望通过这篇博客来一一实现官网的案例（Python版本），对一些运筹学理论进行诠释，并给出一些自己对理论与Solver API的理解。代码使用jupyter重写（.ipynb文件），方便对模块进行解释并演示，详见代码。

1. A few simple applications

facility.py

问题背景是运筹学中经典的UFLP(Uncapacitated facility location Problem)，下图给出wiki上的介绍：

Uncapacitated facility location_wiki

大致解释：
① 该问题是调度问题的拓展，在需求一定要满足的前提下，决策选择哪些供应点，以保证总成本最小化。总成本中包含固定成本与运输成本，一旦供应点被选作供应，就需付出定额的固定成本，运输成本则来自于供应点到需求点的运输。
② 模型中各工厂的需求量一定，都为单位1；变量u表示供给点的最大供应量，其供应不能超过自身能力上限。
③ GUROBI程序中描述的问题与之差别为各需求点的需求有差异，且未归一化到1。
④ 该问题中，需求侧与供给侧的供应关系为full-connected，实际中可能是semi-connected，或涉及物品的种类不止一种等等，这些都属于问题的变种。

原代码在实现中，建立好model后，找到固定成本最高的供给点，让其初始状态为closed，再进行模型求解，为了研究设计初始值的意义及拓展问题，我做了三组实验。

实验一为不添加任何初始条件，直接对问题进行求解，求解结果如下（行表示plant，列表示warehouse）：

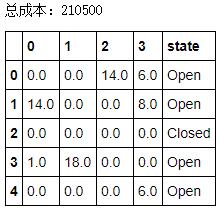
CFLP_sol_one

结果中可看出，最优的选址与配送方案中，plant-2被关闭，而它恰巧是固定成本最高的供给点，因此原代码在求解前将plant-2的初值设为closed，对结果定无影响。因此在第二组实验中，将固定成本最小的plant-0的初值设为closed，其他供给点则设为open，再次进行求解，结果如下：

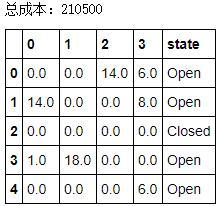
CFLP_sol_two

结果与实验一相同，原因在于初值的设立未改变决策变量的可取范围，故不影响模型的最终求解，而只影响求解过程。GUROBI会根据送入的初值，构建一个可行解，并用该可行解作为Branch and Bound中的初始Bound，Bound较好则可加速Branch and Bound的剪枝过程，提升求解效率（关于B&B算法的解释，可参考MIP Solver Core）。我对两次实验的求解时间做了比较，差距不明显（52ms vs 63ms），原因在于问题规模较小，提速不明显。

现实生活中，由于某些不可抗因素，某些供应点需要强行关闭。针对这一类情况，我设计了实验三，随机选取一个供应点，强制让其在model求解中处于closed状态（前提是剩余的总供应不小于总需求，否则model无解），实现方式有两种：①为变量添加新约束，让其小于等于0；②将决策变量（BINARY类型）的UB设置为0。

1
2
3
4
5
6
# 假设plant-0被选为不采用
# 方式一：
m3.addConstr(open[p] <= 0)
# 方式二：
open[p].UB = 0.0

当plant-1需关闭时，此时model的最优解中，plant-1的状态为closed，总成本上升，求解结果如下：

CFLP_sol_three

补充<1>
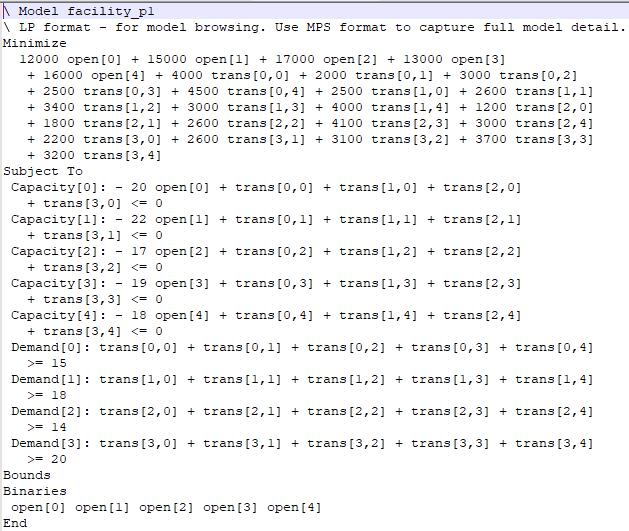
model.write()：该语句能将输入到GUROBI中的model进行输出，便于调试；输出的格式有多种（不同格式对应model中的不同内容），使用较多的是lp文件，它可输出model的数学表达式，如下：

1
m1.write('facility_p1.lp')

输出内容：

CFLP_model

补充<2>
构建约束时尽量避免等式约束，有时目标的优化方向会让约束自动向等号逼近（如问题中对各供给点的供应量）

补充<3>
原程序中，将model的Method参数设置为2，这是在MIP求解中改变对root node的松弛问题的求解方式，与之相似的参数还有NodeMethod，之后会作为一个专门的专题来讲解。

2. Illustrating specific features

sensitivity.py

灵敏性分析侧重于研究模型不确定性对输出结果的影响，不确定性包括多类，有变量不确定性、常量（资源限量、价值常量…）不确定性、约束不确定性等等，这在研究模型鲁棒性、模型各模块与输出的关系等上十分重要。先抛出wiki上的介绍，链接直达：

Sensitivity Analysis

不确定性情况发生时，较直观的想法是修改模型，重新求解。这对复杂的模型很不友好，因反复重新求解需要消耗大量时间。使用GUROBI的好处在于，对模型做部分修改并再次优化时，它能基于上次优化的结果继续求解（原理猜想：基于heuristic，将原模型的最优解修复为增加不确定性后新模型的可行解，得到较好的Upper Bound[in Minimize Problem]，加速Branch and Bound求解过程中的剪枝），快速反映结果，提升效率。

本代码主要研究如何通过GUROBI对决策变量做灵敏度分析，主要关注的决策变量类型为BINARY，BINARY在分析时相对较简单，因为它的取值范围仅有两类，分析时候仅需将0→1或1→0。
我采用’facility.py’中研究的模型作为输入，模型中BINARY变量为供应点的状态(1:open / 0:closed)，在模型求得最优解后，分别改变每个变量的取值，重新求解，观察值的改变对成本目标的影响。下图为最终分析结果：

Sensitivity Analysis Result

从中可以看出，plant-2与plant-4的状态变量的改变对成本目标函数的影响最小。

补充<1>
若需对INTEGER变量做灵敏性分析时，修改的方式与上述类似，通过改变BOUND（LB / UB）或者添加约束限制变量的取值范围。

补充<2>
在coding时，应尽量避免数值误差（虽然GUROBI在这一块已十分完善），如判断BINARY变量的取值是0还是1时，如下：

1
2
open[plant]._origX < 0.5 # True
open[plant]._origX == 0 # False，计算得到的值可能是0.0000...00001